1. 1/3√2 … 1/31,4
а) > +
б) <
в) =
2. В какой функции переменная представляет собой основание:
а) y = 0,4x
б) y = x3 +
в) y = 3x
3. D(ƒ) функции y = (⅓)x =:
а) (0; ⅓)
б) (⅓; +∞)
в) (-∞; + ∞) +
4. Какой поэт сочинил «Оду экспоненте»:
а) Брил +
б) Вийон
в) Киплинг
5. Что не относится к свойствам функции:
а) область определения
б) монотонность
в) возведение степени в квадрат +
6. Как обычно называют функцию y = xx :
а) показательной
б) показательно-степенной +
в) степенной
7. Сколько корней имеет функция 3x = -5:
а) 4
б) 5
в) нет корней +
8. Какое арифметическое действие с показателями степенями нужно выполнить при умножении степеней с одинаковым основанием:
а) сложение +
б) деление
в) вычитание
9. Через какую точку проходят все экспоненты:
а) (0; -1) +
б) (-1; 1)
в) (0; 1) +
10. График какой показательной функции изображен на картинке:
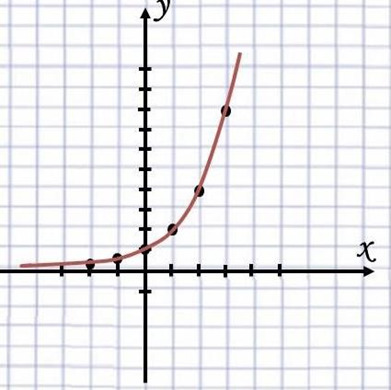
а) y = 0,5x — 1
б) y = 2x +
в) y = 63x
11. (⅓) … 1:
а) < +
б) >
в) =
12. Какая из функций не является показательной:
а) y = (⅙)x
б) y = 4x + 1 +
в) y = 2x
13. Какими свойствами показательная функция не обладает:
а) прерывиста +
б) ограничена снизу
в) не является ни четной, ни нечетной
14. Что является основанием функции y = 4x – 1:
а) x
б) y
в) 4 +
15. Какой знак сравнения ставится между функциями 45x — 1 и 163x + 2 :
а) > +
б) <
в) =
16. С помощью формулы какого математика можно определить показательную функцию комплексного аргумента:
а) Алана Тьюринга
б) Леонарда Эйлера +
в) Анри Пуанкаре
17. Через какую точку проходит график функции y = (⅓)x
а) (-1; 3)
б) (0; 3)
в) (0; 1) +
18. Что является графиком функции y = ax, a > 1:
а) гипербола
б) экспонента +
в) прямая
19. Чему равен x в уравнении 2x — 1 = (⅓):
а) -4
б) 6
в) 2 ½ +
20. При какой степени будет верно равенство в выражении 10x = 100:
а) 2
б) 4 +
в) 3
21. 72 =:
а) 49 +
б) 14
в) 21
22. Какие координаты имеет точка пересечения функций y = (½)x = 1/32:
а) (-1; 1/32)
б) (5; 1/32) +
в) (½; 1/32)
23. Чему равно множество значений функции y = 3x + 1 – 3:
а) (1; 3)
б) (-3; 1)
в) (-3; + ∞) +
24. График какой функции изображен на картинке:
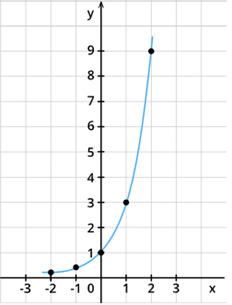
а) y = x + 9
б) y = 3x +
в) y = -2x + 3
25. Функция, заданная формулой y = ax, где a > 0, a ≠ 1, называется:
а) логарифмической
б) тригонометрической
в) показательной +
26. Чему равна область значений функции y = -2x:
а) (-1; 1)
б) (0; + ∞) +
в) (0; — ∞)
27. Какая из функций является показательной:
а) 1,2xx +
б) 2x — 7
в) x — 3
28. В точке с какими показателями пересекаются функции 3x и 4 – x:
а) (-1; 3)
б) (-1; -3)
в) (1; 3) +
29. Функцию вида y=ax, где а>0, a≠1, х – любое число, называют:
а) показательной +
б) степенная
в) логарифмическая
30. Область определения показательной функции: D (y)=R – множество всех действительных чисел, так ли это:
а) нет
б) да +
в) зависит от условий задачи
