1. Найдите производную функции y = x cos x:
а) cos x — x sin x +
б) x — sin x
в) cos x + x sin x
2. Функцией называется:
а) множество всех значений, которые может принимать функция
б) множество всех точек (x; f(x)) на координатной плоскости, где x принадлежит D
в) закон, по которому каждому значению x из множества D ставится в соответствие одно определенное число y +
3. Найдите производную функции y = 4x^3:
а) 12x^3
б) 4x^2
в) 12x^2 +
4. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной, так ли это:
а) нет
б) да +
в) отчасти
5. Производной функции у = f (x) называется:
а) предел приращения аргумента
б) отношение приращения функции к приращению аргумента
в) предел отношения приращения функции к приращению аргумента +
6. Функция f называется убывающей на некотором промежутке:
а) если x2 > x1, то f(x2)=f(x1)
б) если x2 > x1, то f(x2) > f(x1)
в) если x2 > x1, то f(x2) < f(x1) +
7. Найдите производную функции у = x sin x:
а) sin x — x cos x
б) x + x cos x
в) sin x + x cos x +
8. Как называется точка, в которой f ‘(x) меняет знак с ” + ” на ” – “:
а) точка минимума
б) экстремум +
в) точка максимума
9. Найдите производную функции у = 2х + sin x:
а) 2x + cos x
б) 2 — cos x
в) 2 + cos x +
10. Функция f называется нечетной, если для любого х из ее области определения значение -х также принадлежит области определения и верно равенство:
а) f(x)=-f(x)
б) f(-x)=f(x)
в) f(-x)=-f(x) +
11. Найдите производную функции y = 12 — 5x:
а) -5 +
б) 7
в) -5x
12. Вычислите (ax2+bx+c)’:
а) ax+b
б) 2ax+b +
в) ax+b+c
13. Найдите производную функции y = 6x — 11:
а) 6 +
б) -5
в) 6x
14. Уравнение касательной имеет вид:
а) y=f ‘(x0)(x-x0)+f(x0) +
б) y=f ‘(x0)(x+x0)+f(x0)
в) y=f ‘(x0)(x-x0)-f(x0)
15. По данной производной определите исходную функцию и запишите свой ответ: y` = 4 — sin x:
а) y = 4x + cos x +
б) y = 4x — sin x
в) y = 4x — cos x
16. Функция f называется возрастающей на некотором промежутке:
а) если x2 > x1, то f(x2) > f(x1) +
б) если x2 > x1, то f(x2)=f(x1)
в) если x2 > x1, то f(x2) < f(x1)
17. Найдите производную функции f (x) = x sin x:
а) x sin x + cos x
б) x sin x — cos x
в) x cos x + sin x +
18. Понятие дифференциального исчисления, характеризующее скорость изменения функции в данной точке:
а) четная функция
б) производная функции +
в) нечетная функция
19. Геометрический смысл производной состоит в том, что производная равна:
а) синусу угла наклона касательной к графику функции к положительному направлению оси Ох
б) угловому коэффициенту k секущей к графику функции
в) тангенсу угла наклона касательной к графику функции к положительному направлению оси Ох +
20. Сложной функцией считается такая функция, у которой аргумент также является функцией, так ли это:
а) нет
б) да +
в) отчасти
21. Геометрический смысл производной состоит в том, что производная равна:
а) угловому коэффициенту k касательной к графику функции +
б) синусу угла наклона касательной к графику функции к положительному направлению оси Ох
в) угловому коэффициенту k секущей к графику функции
22. Найдите производную функции у = 1–4tgx в точке х0 = 0:
а) -4
б) -3
в) 2
23. Решите уравнение 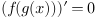 если
если 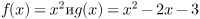
а) 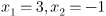
б) 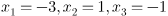
в) 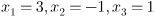 +
+
24. Найдите производную функции у = 3sin x – cos x:
а) у′ = 3cos x – sin x
б) у′ = –3cos x – sin x
в) у′ = 3cos x + sin x +
25. Вычислите 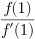 если
если 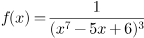
а) 1/3
б) 3
в) -1/3 +
26. Найдите производную функции у = (3х–2)12:
а) у′ = 12(3х–2)11
б) у′ = 36(3х–3)11
в) у′ = 36х(3х–2)11 +
27. Вычислите 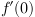 если
если 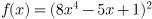
а) -10 +
б) 10
в) 0
28. Даны функции ƒ(х) = 2–3х и g(y) = y2. Какая из следующих функций имеет вид h(x) = g(ƒ(х)) :
а) h(x) = (2–3x)2 +
б) h(x) = 2–9x2
в) h(x) = 2–3x2
29. Найдите область определения функции 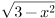
а) 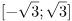 +
+
б) 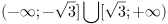
в) 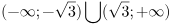
30. Найдите производную функции 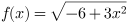
а) 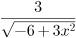
б) 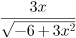 +
+
